Zeitreihenmodelle
Hier basiert die Prognose auf der Grundlage der Analyse einer vorliegenden Zeitreihe, d. h. von Beobachtungswerten, die in gleichem zeitlichen Abstand aufeinander folgen. Es lassen sich folgende Methoden unterscheiden:
Moving Average
Das Modell des gleitenden Durchschnitts basiert auf der Idee, dass die künftige Nachfrage der zuletzt beobachteten Nachfrage ähnelt. Bei diesem Modell geht man einfach davon aus, dass die Prognose der durchschnittlichen Nachfrage der letzten n Perioden entspricht.
Wenn wir diese Idee formalisieren, erhalten wir diese Formel:

Wobei,
ft: die Prognose für den Zeitraum t ist
n: ist die Anzahl der Perioden, aus denen wir den Durchschnitt nehmen
dt: ist die Nachfrage im Zeitraum t
Sobald wir den historischen Zeitraum hinter uns gelassen haben, definieren wir jede zukünftige Prognose einfach als die
letzte Prognose, die auf der Grundlage der historischen Nachfrage berechnet wurde. Das bedeutet, dass bei diesem Modell die Zukunftsprognose flach ist. Dies ist eine der größten Einschränkungen dieses Modells: seine Unfähigkeit, einen Trend zu extrapolieren.
Ein gleitender Durchschnitt unterliegt im Wesentlichen drei Einschränkungen.
1. Kein Trend: Das Modell sieht keinen Trend (und projiziert daher auch keinen).
2. Keine Saisonalität: Das Modell reagiert nicht richtig auf Saisonalität.
3. Flache historische Gewichtung: Ein gleitender Durchschnitt weist allen berücksichtigten alle berücksichtigten historischen Perioden gleich gewichtet
Exponentielle Glättung
Die einfache exponentielle Glättung ist eine der einfachsten Methoden zur Prognose einer Zeitreihe. Einfach wie beim gleitenden Durchschnitt, besteht die Grundidee dieses Modells in der Annahme, dass die Zukunft mehr oder weniger wie die (jüngste) Vergangenheit sein wird. Das einzige Muster, das dieses Modell das dieses Modell aus der Nachfragehistorie lernen kann, ist sein Niveau.
Das Niveau ist der Durchschnittswert, um den die Nachfrage im Laufe der Zeit schwankt.
Das Modell der exponentiellen Glättung prognostiziert dann die zukünftige Nachfrage als seine letzte Schätzung des Niveaus. Es ist wichtig zu verstehen, dass es keine endgültige mathematische Definition des Niveaus gibt, sondern dass es an unserem Modell liegt, es zu schätzen.
Das einfache Modell der exponentiellen Glättung hat einige Vorteile im Vergleich zu gegenüber einem Modell des gleitenden Durchschnitts:
- Das Gewicht, das jeder Beobachtung beigemessen wird, sinkt exponentiell mit der Zeit ab.
Mit anderen Worten: Für die Bestimmung der Prognose hat der jüngste historische Zeitraum die größte Bedeutung; jeder nachfolgende (ältere) Zeitraum hat dann immer weniger Bedeutung.
Dies ist oft besser als Modelle mit gleitendem Durchschnitt, bei denen die gleiche (Gewichtung) einer Handvoll historischer Zeiträume gegeben wird.
- Ausreißer und Rauschen haben weniger Einfluss als bei einer naiven Prognose.
Der Grundgedanke eines jeden exponentiellen Glättungsmodells ist, dass das Modell in jeder Periode Modell in jeder Periode ein wenig von der jüngsten Nachfragebeobachtung lernt und sich an der letzten Vorhersage erinnert. Der Glättungsparameter (oder die Lernrate) alpha (α) bestimmt, wie viel Bedeutung der jüngsten Nachfragebeobachtung beigemessen wird. Lassen Sie uns dies mathematisch darstellen:

Der Clou an dieser Formel ist, dass die letzte Prognose des Modells bereits einen Teil der vorherigen Nachfragebeobachtung und einen Teil der vorherigen Vorhersage. Das bedeutet, dass die vorherige Prognose alles enthält, was das Modell bisher aus der Nachfragehistorie gelernt hat.
α: ist ein Verhältnis (oder ein Prozentsatz), das angibt, wie viel Bedeutung das Modell der jüngsten Beobachtung im Vergleich zur Bedeutung der Nachfragehistorie beimisst.
αdt-1: steht für die Lernrate mal der vorherigen Nachfragebeobachtung. Man könnte sagen, dass das Modell dem letzten Nachfrageereignis eine bestimmte Bedeutung (Alpha) beimisst.
(1 - α)ft-1: gibt an, wie viel sich das Modell von seiner vorherigen Prognose merkt. Man beachte, dass hier die rekursive Magie
stattfindet, da ft-1 selbst definiert wurde als partiell dt-2 und ft-2.
Dieses einfache Modell der exponentiellen Glättung ist etwas intelligenter als das Modell des gleitenden Durchschnitts Modell, da es eine geschickte Gewichtung der historischen Nachfragebeobachtungen vornimmt. Aber es hat immer noch viele Einschränkungen:
- Es kann keine Trends prognostizieren
- Es erkennt keine saisonalen Muster
- Es kann (von Haus aus) keine externen erklärenden Variablen (wie Preisgestaltung oder Marketingausgaben) verwenden
Holt-Winters Modell
Das Holt Winters-Verfahren zählt zu der Familie der exponentiellen Glättungen. Im Rahmen dieser Verfahren muss man sich zunächst der Zeitreihe der Vergangenheitswerte widmen, um herauszufinden welche Methode für das jeweilige Problem am besten funktioniert. Eine Zeitreihe ist die Aufzeichnung von Beobachtungen (Absatzzahlen, Börsenkurse, etc.), die in Perioden gleicher Länge (Jahr, Quartal, Monat, etc.) erhoben werden. Dabei hängt die Wahl der Methode, d.h. welche die zugrundeliegende Zeitreihe am optimalsten nachbilden kann, von der Struktur der Zeitreihe ab.
Man unterscheidet ob die Zeitreihe
• keinen Trend und keine Saisonalität,
• einen Trend, aber keine Saisonalität oder
• einen Trend und eine Saisonalität besitzt.
Das Holt Winters Verfahren berücksichtigt historische Datensätze, die sowohl einen Trend als auch saisonale Einflüsse aufweisen.
Bei dieser Gattung von Prognoseverfahren wird die gegebene Zeitreihe in einzelne Komponenten zerlegt. Je nach Verfahren unterscheidet man zwischen der Niveaukomponente mt, der Trendkomponente bt und der Saisonkomponente st. Mit Hilfe der extrahierten Komponenten kann dann mittels Extrapolation ein Blick auf die gewünschten zukünftigen Perioden geworfen werden. Das Besondere an diesem Verfahren ist, dass man mit Hilfe von Glättungsfaktoren die zeitlich älter werdenden Beobachtungen gewichtet, um somit zu entscheiden, ob der jüngeren oder der älteren Vergangenheit größere Aufmerksamkeit geschenkt werden muss. Je nachdem wie viele Komponenten extrahiert werden, spricht man von
• der einfachen exponentiellen Glättung (Niveaukomponente),
• der doppelten exponentiellen Glättung (Niveau- und Trendkomponente) und
• der dreifachen exponentiellen Glättung oder Holt Winters Verfahren (Niveau-, Trend- und Saisonkomponente).
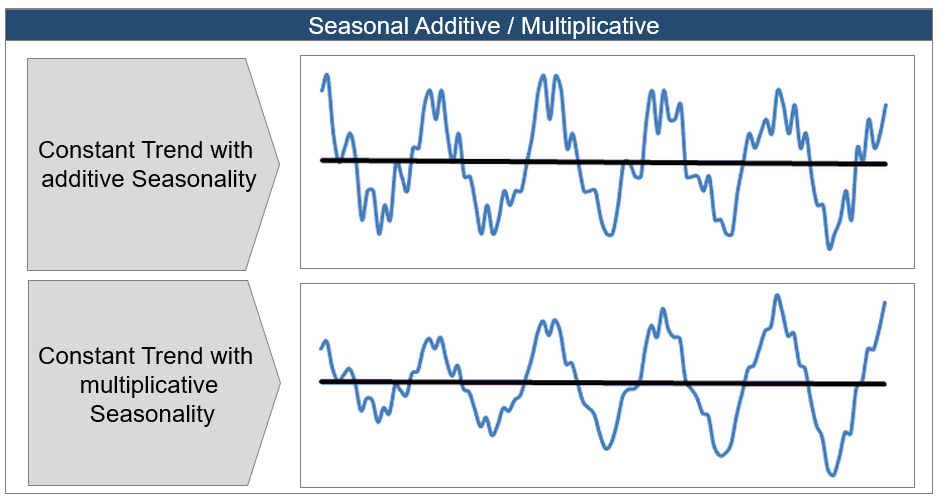
Beim Holt Winters-Verfahren unterscheidet man zusätzlich, ob es sich um einen additiven oder einen multiplikativen Ansatz handelt.
ARIMA-Modell
Das ARIMA-Modell ist ebenfalls ein sehr weit verbreitetes Verfahren in der Zeitreihenmodellierung. Box und Jenkins haben es als erstes formuliert, wobei es eine Erweiterung des ARMA-Modells darstellt. Diese Ausweitung war notwendig, weil viele ökonomische Zeitreihen aufgrund der Stationaritätsbedingung nicht bearbeitet werden konnten. Gerade die Absatzzahlen verschiedenster Produkte in Unternehmen weisen gewisse Trends auf bzw. sind saisonalen Schwankungen ausgesetzt und können deshalb nicht stationär sein. Das ARIMA-Modell stellt hierbei eine Möglichkeit dar auch solche Zeitreihen zu modellieren und somit Zukunftsprognosen zu formulieren. ARIMA bedeutet ausgesprochen autoregressiv (AR) integrated (I) moving average (MA).
Croston-Verfahren
Die Vorhersage von Produkten mit intermittierender Nachfrage ist kompliziert. An dieser Stelle wird das speziell für die Prognose solcher Zeitreihen entwickelte Modell von Croston vorgestellt.
Seine Idee lässt sich in drei einfachen Schritten zusammenfassen:
- Bewertung der durchschnittlichen Nachfrageniveaus bei Auftreten einer Nachfrage.
- Bewertung der durchschnittlichen Zeit zwischen zwei Nachfrageereignissen.
- Prognostizieren Sie die Nachfrage als das Nachfrageniveau (bei Auftreten eines Ereignisses) multipliziert mit der Wahrscheinlichkeit eines Ereignisses.
© Urheberrecht. Alle Rechte vorbehalten.
Wir benötigen Ihre Zustimmung zum Laden der Übersetzungen
Wir nutzen einen Drittanbieter-Service, um den Inhalt der Website zu übersetzen, der möglicherweise Daten über Ihre Aktivitäten sammelt. Bitte überprüfen Sie die Details in der Datenschutzerklärung und akzeptieren Sie den Dienst, um die Übersetzungen zu sehen.